Finite Faults

Finite Faults, Past 1 Year

View Map and List of Finite-Fault Events

  • Search Finite-Fault Archives

    Search for events that include Finite Faults. The Search form link from here is already configured to return only events with Finite-Fault products. You enter additional search parameters. The default time window is the past 30 days.

    Downloadable Files

    For each finite-fault model posted on the USGS earthquake website, a series of downloadable files are included:

    • Finite-Fault Model Maps – Map representation of the finite-fault model, in GEOJSON and PNG formats.
    • Data and Model Fits (previously called Wave Plots) – Plots seismic and/or geodetic observations and model fits used in the inversion, in PNG format contained within a ZIP archive.
    • CMT Solution - Full CMT solution for every point in the finite-fault region, in CMTSOLUTION ASCII text format (Dziewonski, Chou, & Woodhouse, 1981; http://globalcmt.org).
    • Inversion Parameters – Files of inversion parameters for the finite fault, in both a static PARAM ASCII text format familiar to users of rapid NEIC fault models, and in the SRCMOD Finite Source Parameter (FSP) ASCII text format (Mai et al., 2016).
    • Coulomb Input File – Input file for the Coulomb3 software package, in INP ASCII text format (Toda et al., 2011; http://earthquake.usgs.gov/research/software/coulomb/).
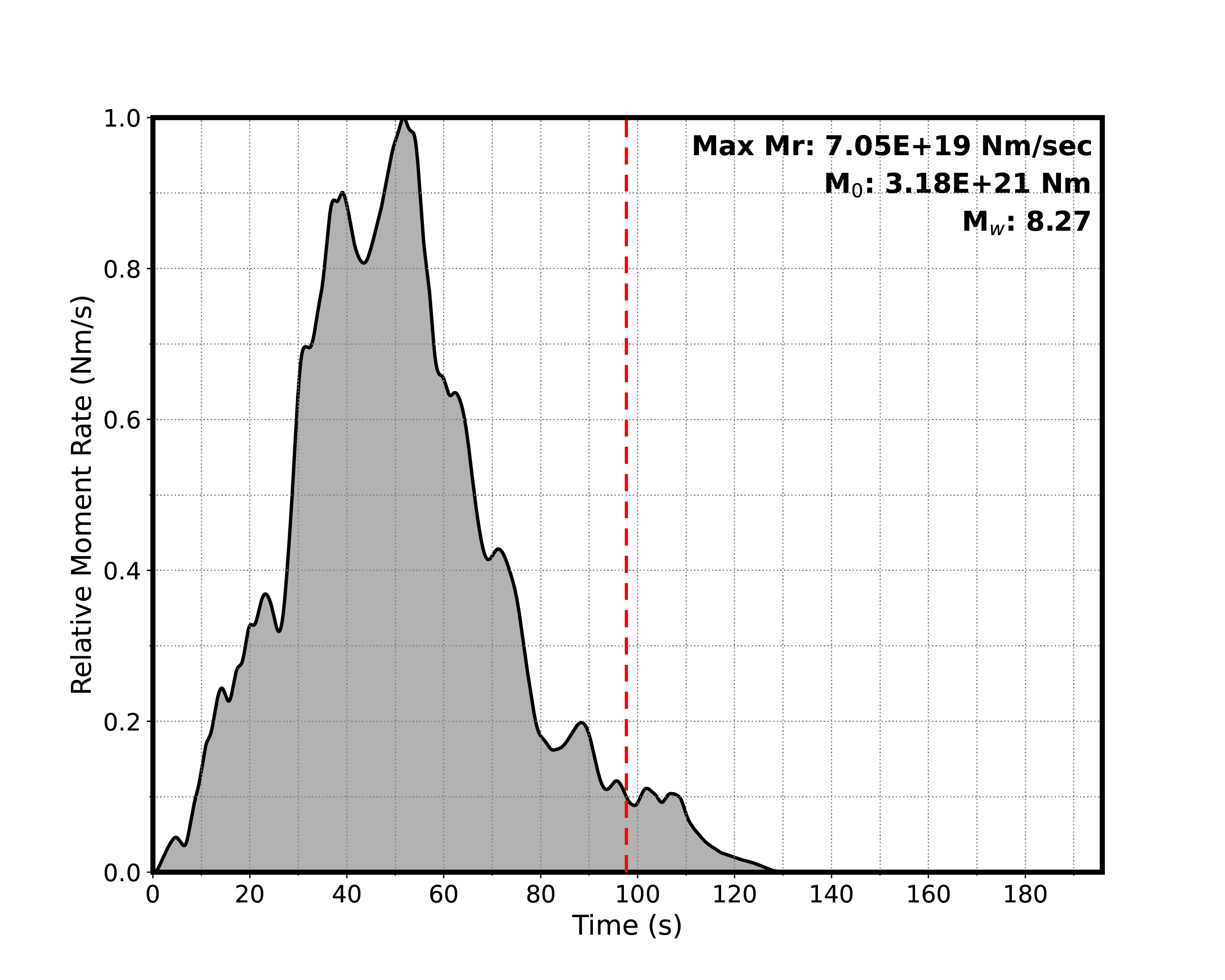
    • Moment Rate Function Files – Source time function for the event, in tabular ASCII text format and plot in PNG format.
    • Surface Deformation File - Surface displacement represented as three-components of predicted ground deformation, calculated using the Okada (1992) formulation, in tabular ASCII text format.
    • ShakeMap Rupture Polygon File – Geometry of finite fault’s rectangular slipped area, which is used as input to ShakeMap, in ASCII text format.
    • Resampled Interferogram - the resampled Interferometric Synthetic Aperture Radar (InSAR) line-of-sight surface displacement observations (available if InSAR is included in the finite-fault model), in ASCII text format, contained within a ZIP file.

Introduction to Finite-Fault Models

Earthquakes occur when there is sudden slip along a fault. Although earthquakes are most often plotted as points on a map, fault slip occurs along discrete fault surfaces that have length and width. The magnitude of an earthquake is partially determined by the area of the fault that moved and how much it moved (the slip amplitude). The seismic moment, the value seismologists use to describe the size on an earthquake, is simply the product of average slip, fault area, and shear modulus - a variable related to the strength of rock in the earthquake source region. The moment magnitude (Mw) is derived from seismic moment and is the most common type of magnitude reported for earthquakes today. The fault dimensions (length and width) and the amount of slip vary dramatically across the spectrum of earthquake magnitudes. For example, an Mw 4 earthquake fault commonly has a length of around 1 km, an Mw 7 earthquake has a length of around 40 km, and the 2004 Mw 9.1 Sumatra earthquake had a rupture length of over 1000 km.

Many factors determine the nature of shaking that is produced in the various regions around an earthquake, including the amount, rate, and location of slip. Since the shaking caused by an earthquake – and thus the impact it has on people and infrastructure – is related to the size of the area and amount of slip on the fault, constraining the slip history (what slipped and how much and when during the complete rupture) of an earthquake is an important step for earthquake response at the National Earthquake Information Center (NEIC), to improve our real time estimates of earthquake shaking (ShakeMap) and related fatalities and loses (PAGER).

The dimensions of the fault and slip amplitude along the fault that produced an earthquake can be represented in a “finite-fault model.” This model of an earthquake is generated through a “finite-fault inversion,” which uses ground motion observations of the earthquake (e.g., seismic waveforms, static displacements) to estimate where, when, and how much slip occurred. Typically, a simplified fault plane is divided into multiple sub-faults, and the inversion estimates the amount of slip on each sub-fault.

map of Chile and ocean with a grid with colors overlain
Example finite-fault model for the September 16, 2015, Mw8.3 Illapel, Chile, earthquake. The fault plane over which slip is modeled is outlined in black, with the red line indicating the up-dip edge, next to the Peru-Chile trench (thick white line) where the Nazca plate (west of the trench) subducts beneath the South America plate (east of the trench). The fault dips eastward at 19° toward the east, following the interface between the two tectonic plates. The black-outlined star represents the earthquake hypocenter, or the initial location of slip along the fault. The colorbar denotes the amount of slip modeled at each sub-fault, the smaller squares that make up the fault. White inverted triangles show the locations of nearby strong-motion accelerometer stations. Blue triangles show the locations of nearby high-rate Global Navigation Satellite Systems (HR GNSS) stations. Static GNSS observations (black arrows) are shown in comparison to static synthetic GNSS (red arrows), where “synthetic” indicates the model prediction. In a good model, the black observations and red synthetic model fits will be similar. (Figure adapted from Goldberg et al., 2022a)

The resulting finite-fault models can be static, meaning that we estimate only the slip amplitudes and locations of slip, or kinematic, meaning that we also estimate the timing of slip. Kinematic models allow seismologists to estimate the source-time-function of an earthquake, or how seismic moment was released over the duration of the earthquake, and these models require geophysical measurements that capture how the earthquake evolved as it ruptured. In both static and kinematic models, the sum of the moment released on each subfault is equivalent to the total seismic moment, M0, of the earthquake. The earthquake magnitude, Mw, is related to seismic moment by: Mw= 2/3 (log10⁡(M0)-9.1).

plot that looks like a steep gray mountain
Source time function of the 2015 Mw8.3 Illapel, Chile, earthquake. The dashed red line denotes the interpreted end of the event, attributing modeled moment release after this point to fitting of waveform noise. This model suggests that the earthquake reached peak moment rate (Mr) at about 50 seconds. The total seismic moment (M0) and equivalent magnitude (Mw) correspond to the overall size of the earthquake. (From Goldberg et al., 2022a).

Scientific Details on Data Processing and Inversion

Finite-fault models generated by the USGS NEIC generally employ a kinematic finite-fault inversion approach based on the method of Ji et al. (2002), which carries out the inversion in the wavelet domain. Starting fault geometries are typically aligned with estimates from a Centroid Moment Tensor (CMT), either the USGS W-phase (Hayes et al., 2009) or Global CMT (Dziewonski, Chou, & Woodhouse, 1981; globalcmt.org) solution. A moment tensor solution has two potential fault plane orientations; one is the causative fault plane, and the other the auxiliary plane. The causative fault plane is the one that slipped to produce the earthquake, while the auxiliary plane is a mathematically viable solution but does not correspond to the physical event itself. In some cases, prior knowledge of the tectonic environment allows us to make an informed decision about which plane is the causative fault plane. Otherwise, both possible fault planes of the initial CMT solution are tested to account for the uncertainty regarding which plane describes the causative fault. We may then systematically vary the strike and dip of the initial geometry to test model sensitivity to these orientations or make slight variations to the fault plane orientation to fit a mapped fault geometry in the region of interest. We may further divide a favored plane into multiple fault segments if required by the data or suggested by external information.

Rupture velocity is the velocity at which the earthquake rupture front propagates across the fault plane. In the finite-fault model, rupture velocity can be fixed or allowed to vary. To account for unknown rupture characteristics, we generally test a broad distribution of fixed velocities, before settling on a final model where rupture velocity is allowed to fluctuate about a favored fixed value.

We estimate the initial fault length from empirical relationships between duration and moment (Blaser et al., 2011), scaled to length assuming a rupture velocity (generally 2.5 km/s), and multiplied by 3.3 to account for uncertainty in rupture characteristics. We generate Green's functions using the frequency-wavenumber algorithm of Zhu & Rivera (2001). Mathematically, Green’s functions are the displacements produced by an impulse force. For the purpose of finite-fault inversions, the Green’s functions relate a unit of slip at a sub-fault to the resulting ground motion that would be observed at a seismic station. To calculate that response, we use a one-dimensional seismic velocity model based on the PREM (Dziewonski & Anderson, 1981) and LITH1.0 (Pasyanos et al., 2014) global velocity models. In regions where seismic velocity structure has been well-studied, we may substitute a more detailed local velocity model from published studies.

We divide the fault planes into a series of sub-faults along the strike and dip directions, and the inversion uses a simulated annealing approach to simultaneously solve for the slip amplitude, slip direction, rise time (the local duration of rupture), and rupture initiation time of each sub-fault, where sub-fault source time functions are modeled with an asymmetric cosine function (Ji et al., 2002, 2003; Koch et al., 2019).

The model is referenced spatially to the preferred hypocenter, at least initially. As with other key parameters, hypocenter location is adjusted when other information (e.g., published relocation studies) indicates a necessary recalculation.

The inversion procedure uses teleseismic body wave (P and SH observations 30-90 degrees from the source, bandpass-filtered typically between 1 and 200 s) and surface wave (Rayleigh and Love, typically bandpass-filtered between 200 and 500 s) data on a fault surface defined a priori. For each inversion, we choose to include data sampling a range of azimuths from the source, while avoiding data with small signal-to-noise ratios or poor-quality observations.

waveforms
Example teleseismic waveform observations (black) and model synthetic fits (red) for broadband station DGMT. a) P wave, b) SH wave, c) Rayleigh (Z) wave, d) Love (T) wave. Numbers to the left denote station azimuth (top) and distance in degrees (bottom). Numbers to the right denote the maximum amplitude of the observed waveform (black) and synthetic model fit (red). (Adapted from Goldberg et al., 2022b)

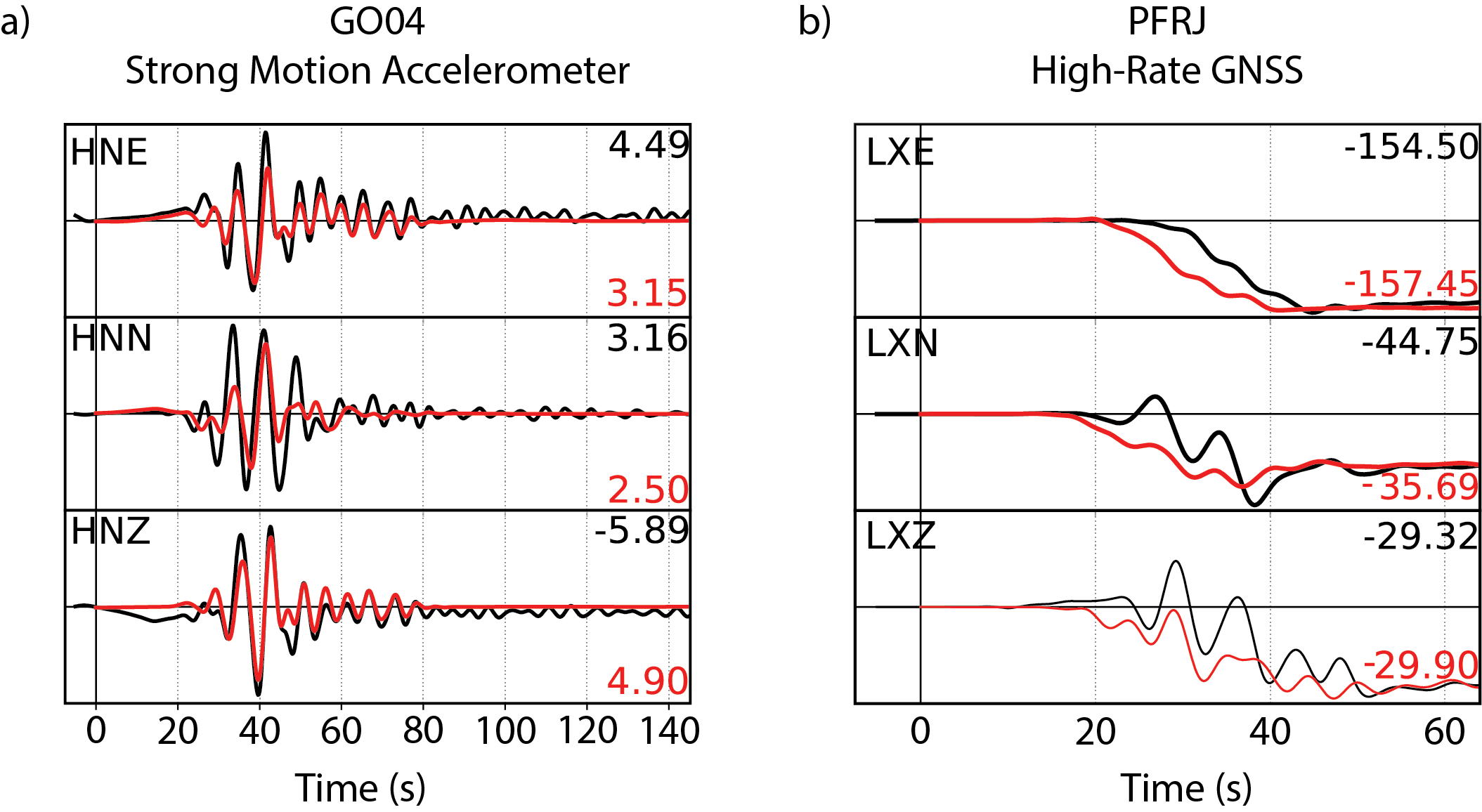
When available, we incorporate regional seismic and geodetic data (strong-motion accelerometer, Global Navigation Satellite Systems [GNSS], and/or Interferometric Synthetic Aperture Radar [InSAR]) into the inversion as well (Goldberg et al., 2022). Accelerometer waveforms are typically bandpass-filtered between 8 and 100 s. GNSS displacements are obtained in real-time or post-processed once final clocks and orbits become available (e.g., Melbourne et al., 2021; Bertiger et al., 2020; Herring et al., 2018).

waveforms and plots
Example local waveform observations (black) and model synthetic fits (red). a) Strong motion accelerometer station and b) High-rate GNSS station waveforms in the east (top), north (center), and vertical (bottom) components of motion. Numbers to the right denote the maximum amplitudes (in centimeters/second for the accelerometers and centimeters for HR GNSS) for the observed and synthetic waveforms in black and red, respectively. (Adapted from Goldberg et al., 2022a)

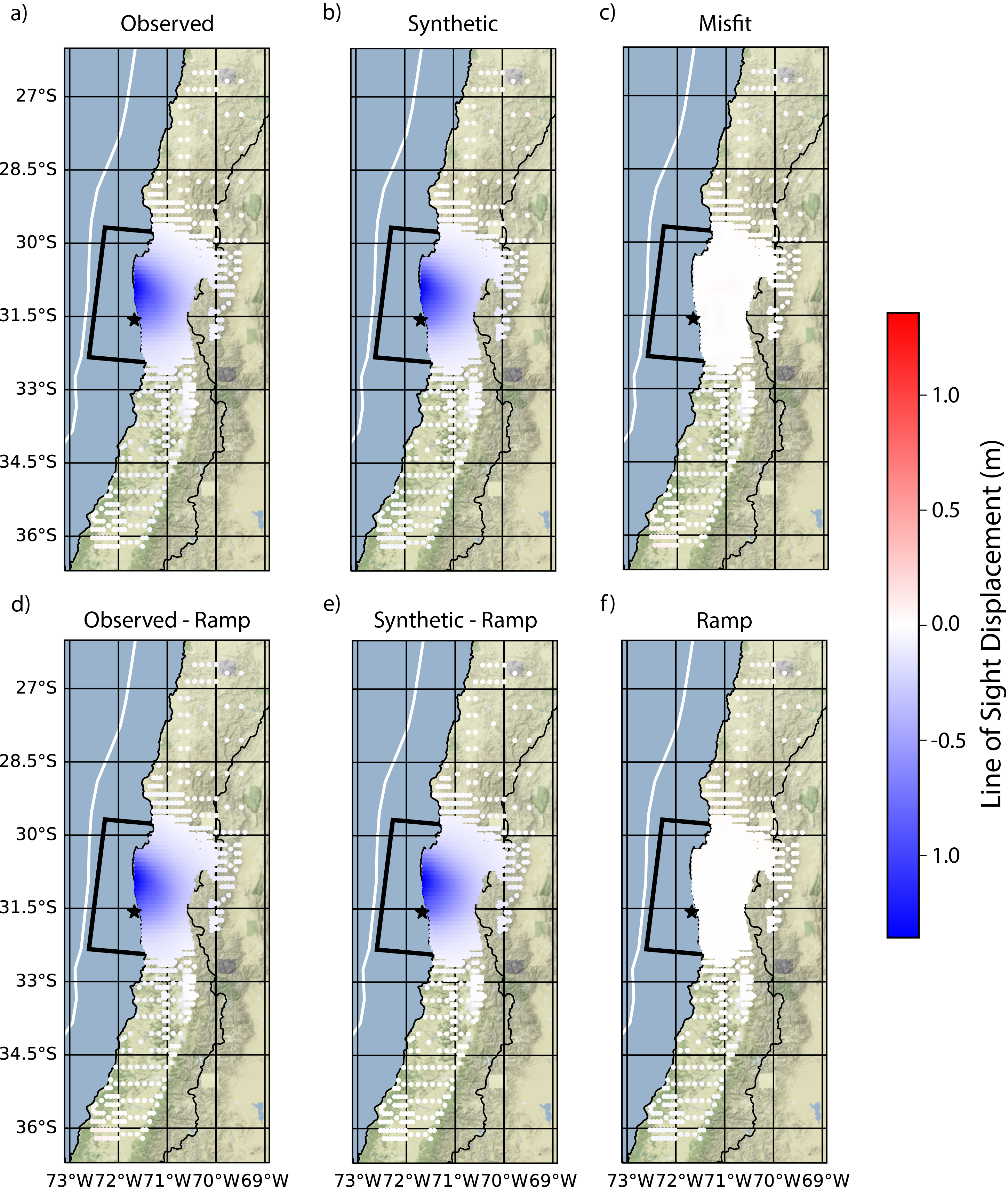
InSAR interferograms are processed with the InSAR Scientific Computing Environment (Rosen et al., 2018) package and resampled using the approach of Lohman & Simons (2005). InSAR observations may become available within hours to days after the earthquake and are generally incorporated into NEIC finite-fault models as updates in the weeks following the event. Often, long-wavelength artifacts, introduced by imprecise satellite orbit positions, result in processed interferograms showing unphysical deformation at far-field distances. This long-period signal (known as a ramp) must be disentangled from the true earthquake deformation signal. The ramp signal is solved for simultaneously during the simulated annealing procedure.

6 sidebyside maps
Interferometric Synthetic Aperture Radar (InSAR) observations and inversion solution. a) Downsampled line of sight displacements, b) model synthetic line of sight displacements, c) misfit between observed and synthetic line of sight displacements, d) observed line of sight displacement with ramp removed, d) model synthetic line of sight displacement with ramp removed, f) linear ramp solution. Earthquake hypocenter is denoted by the black star, with fault outline in black. (Adapted from Goldberg et al., 2022b)

For more details on this approach and our results for past earthquakes, see Hayes (2017) and Goldberg et al. (2022a).

References

  • Bertiger, W., Y. Bar-Sever, A. Dorsey, B. Haines, N. Harvey, D. Hemberger, et al. (2020). GipsyX/RTGx, a new tool set for space geodetic operations and research. Adv. Space Res., 66(3), 469–489, doi: 10.1016/ j.asr.2020.04.015.
  • Blaser, L., F. Krüger, M. Ohrnberger, and F. Scherbaum (2010). Scaling relations of earthquake source parameter estimates with special focus on subduction environment. Bull. Seismol. Soc. Am., 100(6), 2914–2926, doi: 10.1785/0120100111.
  • Dziewonski, A. M. and. D. L. Anderson (1981). Preliminary reference Earth model. Phys. Earth Planet. Int., 25(4), 297–356, doi: 10.1016/0031-9201(81)90046-7.
  • Dziewonski, A. M., T.-A. Chou, and J. H. Woodhouse (1981). Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res.: Solid Earth, 86(B4), 2825–2852, doi: 10.1029/JB086iB04p02825.
  • Goldberg, D. E., P. Koch, D. Melgar, S. Riquelme, and W. L. Yeck (2022a). Beyond the teleseism: Introducing regional seismic and geodetic data into routine USGS finite‐fault modeling. Seismol. Res. Lett., 93(6), 3308–3323, doi: 10.1785/0220220047.
  • Goldberg, D. E., W. D. Barnhart, and B. W. Crowell (2022b). Regional and teleseismic observations for finite-fault product. U.S. Geological Survey data release, doi: 10.5066/P9ZO5FRS.
  • Hayes, G. P., L. Rivera, and H. Kanamori (2009). Source inversion of the W-Phase: Real-time implementation and extension to low magnitudes. Seismol. Res. Lett., 80(5), 817–822. doi: 10.1785/gssrl.80.5.817.
  • Hayes, G. P. (2017). The finite, kinematic rupture properties of great-sized earthquakes since 1990. Earth Planet. Sci. Lett., 468, 94–100, doi: 10.1016/j.epsl.2017.04.003.
  • Herring, T. A., R. W. King, and S. C. McClusky (2018). Introduction to GAMIT/GLOBK, Release 10.7. Massachusetts Institute of Technology: Cambridge, Massachusetts, 54 pp.
  • Ji, C., D. J. Wald, and D. V. Helmberger (2022). Source description of the 1999 Hector Mine, California earthquake; Part I: Wavelet domain inversion theory and resolution analysis. Bull. Seism. Soc. Am., 92(4), 1192–1207, doi: 10.1785/0120000916.
  • Ji, C., D. V. Helmberger, D. J. Wald, and K. F. Ma (2003). Slip history and dynamic implications of the 1999 Chi-Chi, Taiwan, earthquake. J. Geophys. Res.: Solid Earth, 108(B9), 2412, doi: 10.1029/2002JB001764.
  • Koch, P., F. Bravo, S. Riquelme, and J. G. Crempien (2019). Near‐real‐time finite‐fault inversions for large earthquakes in Chile using strong‐motion data. Seismol. Res. Lett., 90(5), 1971–1986, doi: 10.1785/0220180294.
  • Melbourne, T. I., W. M. Szeliga, V. Marcelo Santillan, and C. W. Scrivner (2021). Global Navigational Satellite System seismic monitoring. Bull. Seismol. Soc. Am., 111(3), 1248–1262, doi: 10.1785/0120200356.
  • Pasyanos, M. E., T. G. Masters, G. Laske, and Z. Ma (2014). LITHO1.0: An updated crust and lithospheric model of the Earth. J. Geophys. Res.: Solid Earth, 119(3), 2153–2173, doi: 10.1002/2013JB010626.
  • Rosen, P. A., E. M. Gurrola, P. Agram, J. Cohen, M. Lavalle, et al. (2018). The InSAR scientific computing environment 3.0: A flexible framework for NISAR operational and user-led science processing, Proc. of the 2018 IEEE Int. Geoscience and Remote Sensing Symposium, 4897–4900, doi: 10.1109/IGARSS.2018.8517504.
  • Toda, S., R. S. Stein, V. Sevilgen, and J. Lin (2011). Coulomb 3.3 Graphic-rich deformation and stress-change software for earthquake, tectonic, and volcano research and teaching—user guide. U.S. Geological Survey Open-File Report 2011–1060, 63 pp., doi: 10.3133/ofr20111060.
  • Zhu, L. and L. A. Rivera (2002). A note on the dynamic and static displacements from a point source in multilayered media. Geophys. J. Int., 148(3), 619–627, doi: 10.1046/j.1365-246X.2002.01610.x.