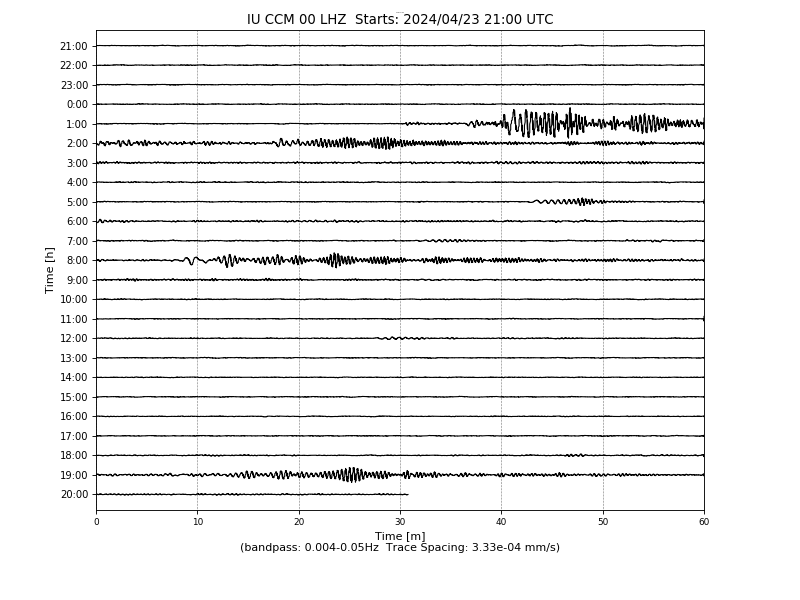
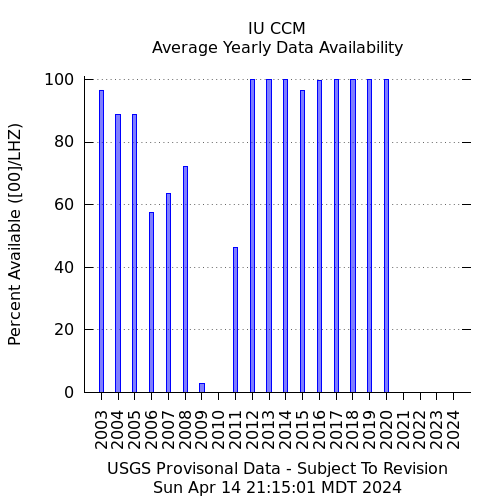
Cathedral Cave, Missouri, USA
IU CCM commences operations on: 1989,209
| Host | St. Louis University |
|---|---|
| Network | IU |
| Latitude | 38.056 |
| Longitude | -91.245 |
| Elevation | 172 |
| Datalogger | Q330-HR |
| Broadband | Streckeisen STS-6A VBB Seismometer |
| Accelerometer | Kinemetrics FBA ES-T EpiSensor Accelerometer |
| Telemetry Status at the NEIC | Pending |
 Jump to Navigation
Jump to Navigation