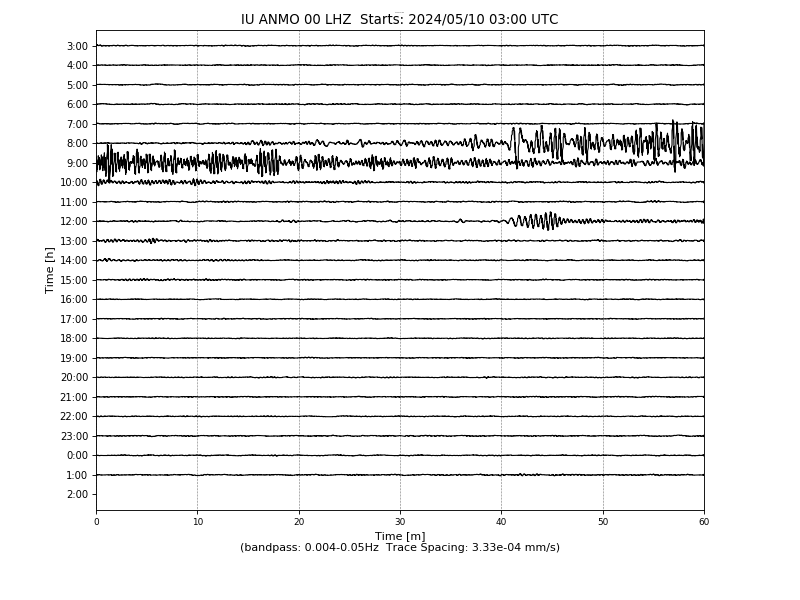
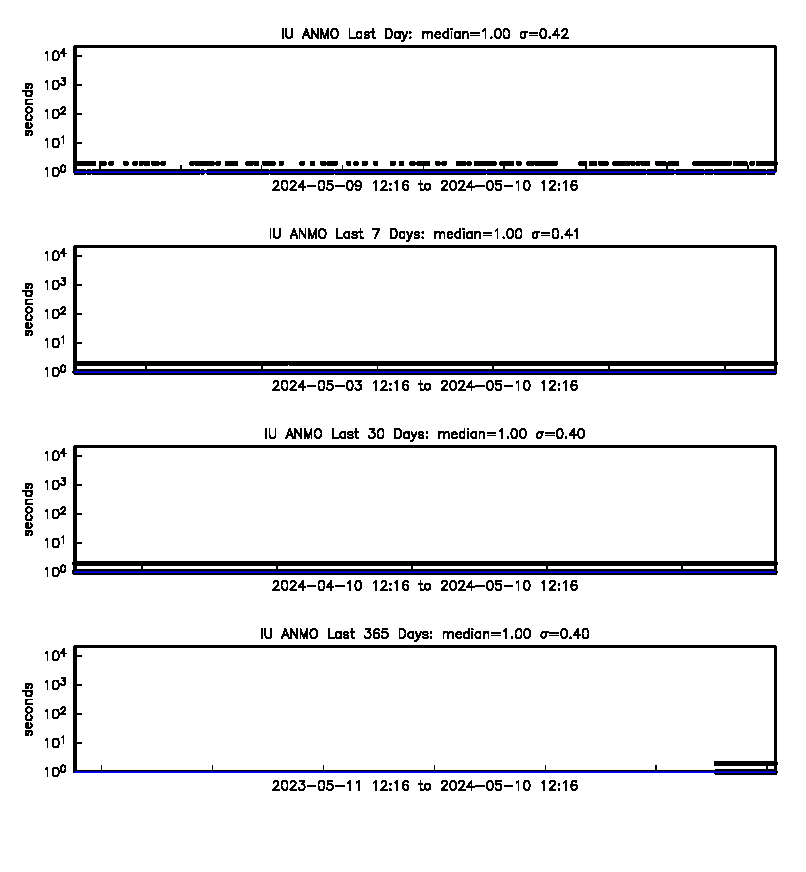
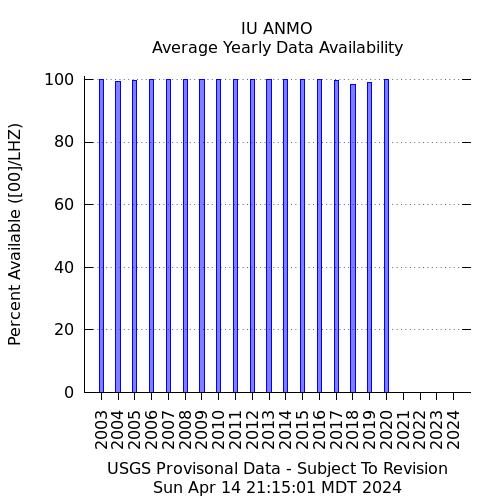
Albuquerque, New Mexico, USA
IU ANMO commences operations on: 1989,241
| Host | US Geological Survey |
|---|---|
| Network | IU |
| Latitude | 34.946 |
| Longitude | -106.457 |
| Elevation | 1816 |
| Datalogger | Q330-HR |
| Broadband | Streckeisen STS-6A VBB Seismometer |
| Accelerometer | Titan Accelerometer |
| Telemetry Status at the NEIC | Pending |
 Jump to Navigation
Jump to Navigation