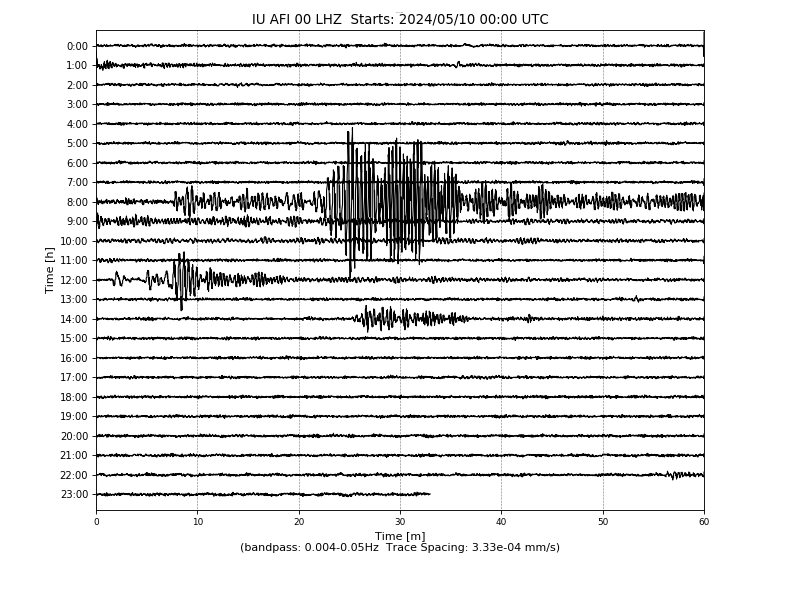
Afiamalu, Samoa
IU AFI commences operations on: 1993,236
| Host | Ministry of Natural Resources and Environment |
|---|---|
| Network | IU |
| Latitude | -13.909 |
| Longitude | -171.783 |
| Elevation | 706 |
| Datalogger | Q330-HR |
| Broadband | Streckeisen STS-6A VBB Seismometer |
| Accelerometer | Kinemetrics FBA ES-T EpiSensor Accelerometer |
| Telemetry Status at the NEIC | Pending |
 Jump to Navigation
Jump to Navigation