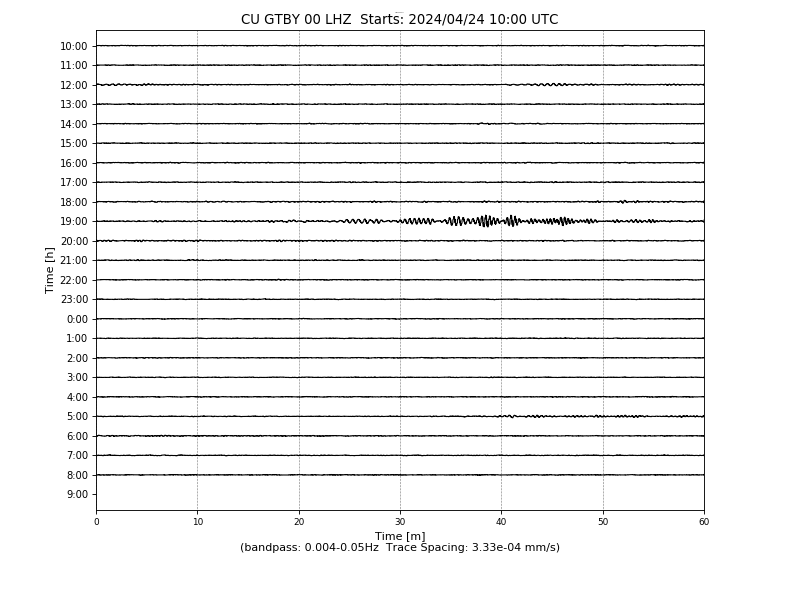
Guantanamo Bay, Cuba
CU GTBY commences operations on: 2007,239
| Host | US Navy |
|---|---|
| Network | CU |
| Latitude | 19.927 |
| Longitude | -75.111 |
| Elevation | 79 |
| Datalogger | Q330 |
| Broadband | Streckeisen STS-2.5 |
| Accelerometer | Kinemetrics FBA ES-T EpiSensor Accelerometer |
| Telemetry Status at the NEIC | Pending |
 Jump to Navigation
Jump to Navigation