Extremely Efficient Bayesian Inversions (or how to fit a model to data without the model or the data)
Sarah Minson
U.S. Geological Survey
- Date & Time
- Location
- Online-only seminar via Microsoft Teams
- Host
- Ben Brooks
- Summary
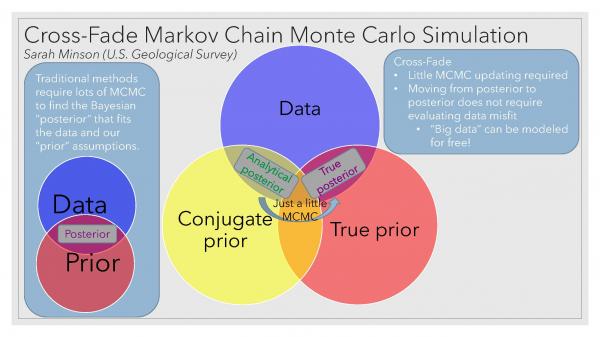
There are many underdetermined geophysical inverse problems. For example, when we try to infer earthquake fault slip, we find that there are many potential slip models that are consistent with our observations and our understanding of earthquake physics. One way to approach these problems is to use Bayesian analysis to infer the ensemble of all potential models that satisfy the observations and our prior knowledge. In Bayesian analysis, our prior knowledge is known as the prior probability density function or prior PDF, the fit to the data is the data likelihood function, and the target PDF that satisfies both the prior PDF and data likelihood function is the posterior PDF.
Simulating a posterior PDF can be computationally expensive. Typical earthquake rupture models with 10 km spatial resolution can require using Markov Chain Monte Carlo (MCMC) to draw tens of billions of random realizations of fault slip. And now new technological advancements like LiDAR provide enormous numbers of laser point returns that image surface deformation at submeter scale, exponentially increasing computational cost. How can we make MCMC sampling efficient enough to simulate fault slip distributions at sub-meter scale using “Big Data”?
We present a new MCMC approach called cross-fading in which we transition from an analytical posterior PDF (obtained from a conjugate prior to the data likelihood function) to the desired target posterior PDF by bringing in our physical constraints and removing the conjugate prior. This approach has two key efficiencies. First, the starting PDF is by construction “close” to the target posterior PDF, requiring very little MCMC to update the samples to match the target. Second, all PDFs are defined in model space, not data space. The forward model and data misfit are never evaluated during sampling, allowing models to be fit to Big Data with zero computational cost. It is even possible, without additional computational cost, to incorporate model prediction errors for Big Data, that is, to quantify the effects on data prediction of uncertainties in the model design. While we present earthquake models, this approach is flexible and can be applied to many geophysical problems.
Closed captions are typically available a few days after the seminar. To turn them on, press the ‘CC’ button on the video player. For older seminars that don’t have closed captions, please email us, and we will do our best to accommodate your request.
 Jump to Navigation
Jump to Navigation